NLP From Scratch: Classifying Names with a Character-Level RNN

Author: Sean Robertson

We will be building and training a basic character-level RNN to classify words. This tutorial, along with the following two, show how to do preprocess data for NLP modeling “from scratch”, in particular not using many of the convenience functions of torchtext, so you can see how preprocessing for NLP modeling works at a low level.

A character-level RNN reads words as a series of characters - outputting a prediction and “hidden state” at each step, feeding its previous hidden state into each next step. We take the final prediction to be the output, i.e. which class the word belongs to.

Specifically, we’ll train on a few thousand surnames from 18 languages of origin, and predict which language a name is from based on the spelling:

$ python predict.py Hinton
(-0.47) Scottish
(-1.52) English
(-3.57) Irish

$ python predict.py Schmidhuber
(-0.19) German
(-2.48) Czech
(-2.68) Dutch

Recommended Reading:

I assume you have at least installed PyTorch, know Python, and understand Tensors:

• https://pytorch.org/ For installation instructions
• Deep Learning with PyTorch: A 60 Minute Blitz to get started with PyTorch in general
• Learning PyTorch with Examples for a wide and deep overview
• PyTorch for Former Torch Users if you are former Lua Torch user

It would also be useful to know about RNNs and how they work:

• The Unreasonable Effectiveness of Recurrent Neural Networks shows a bunch of real life examples
• Understanding LSTM Networks is about LSTMs specifically but also informative about RNNs in general

Preparing the Data

Note

Download the data from here and extract it to the current directory.

Included in the data/names directory are 18 text files named as “[Language].txt”. Each file contains a bunch of names, one name per line, mostly romanized (but we still need to convert from Unicode to ASCII).

We’ll end up with a dictionary of lists of names per language, {language: [names ...]}. The generic variables “category” and “line” (for language and name in our case) are used for later extensibility.

from __future__ import unicode_literals, print_function, division
from io import open
import glob
import os

def findFiles(path): return glob.glob(path)

print(findFiles('data/names/*.txt'))

import unicodedata
import string

all_letters = string.ascii_letters + " .,;'"
n_letters = len(all_letters)

# Turn a Unicode string to plain ASCII, thanks to https://stackoverflow.com/a/518232/2809427
def unicodeToAscii(s):
    return ''.join(
        c for c in unicodedata.normalize('NFD', s)
        if unicodedata.category(c) != 'Mn'
        and c in all_letters
    )

print(unicodeToAscii('Ślusàrski'))

# Build the category_lines dictionary, a list of names per language
category_lines = {}
all_categories = []

# Read a file and split into lines
def readLines(filename):
    lines = open(filename, encoding='utf-8').read().strip().split('\n')
    return [unicodeToAscii(line) for line in lines]

for filename in findFiles('data/names/*.txt'):
    category = os.path.splitext(os.path.basename(filename))[0]
    all_categories.append(category)
    lines = readLines(filename)
    category_lines[category] = lines

n_categories = len(all_categories)

Out:

['data/names/Arabic.txt', 'data/names/Chinese.txt', 'data/names/Czech.txt', 'data/names/Dutch.txt', 'data/names/English.txt', 'data/names/French.txt', 'data/names/German.txt', 'data/names/Greek.txt', 'data/names/Irish.txt', 'data/names/Italian.txt', 'data/names/Japanese.txt', 'data/names/Korean.txt', 'data/names/Polish.txt', 'data/names/Portuguese.txt', 'data/names/Russian.txt', 'data/names/Scottish.txt', 'data/names/Spanish.txt', 'data/names/Vietnamese.txt']
Slusarski

Now we have category_lines, a dictionary mapping each category (language) to a list of lines (names). We also kept track of all_categories (just a list of languages) and n_categories for later reference.

print(category_lines['Italian'][:5])

Out:

['Abandonato', 'Abatangelo', 'Abatantuono', 'Abate', 'Abategiovanni']

Turning Names into Tensors

Now that we have all the names organized, we need to turn them into Tensors to make any use of them.

To represent a single letter, we use a “one-hot vector” of size <1 x n_letters>. A one-hot vector is filled with 0s except for a 1 at index of the current letter, e.g. "b" = <0 1 0 0 0 ...>.

To make a word we join a bunch of those into a 2D matrix <line_length x 1 x n_letters>.

That extra 1 dimension is because PyTorch assumes everything is in batches - we’re just using a batch size of 1 here.

import torch

# Find letter index from all_letters, e.g. "a" = 0
def letterToIndex(letter):
    return all_letters.find(letter)

# Just for demonstration, turn a letter into a <1 x n_letters> Tensor
def letterToTensor(letter):
    tensor = torch.zeros(1, n_letters)
    tensor[0][letterToIndex(letter)] = 1
    return tensor

# Turn a line into a <line_length x 1 x n_letters>,
# or an array of one-hot letter vectors
def lineToTensor(line):
    tensor = torch.zeros(len(line), 1, n_letters)
    for li, letter in enumerate(line):
        tensor[li][0][letterToIndex(letter)] = 1
    return tensor

print(letterToTensor('J'))

print(lineToTensor('Jones').size())

Out:

tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0.]])
torch.Size([5, 1, 57])

Creating the Network

Before autograd, creating a recurrent neural network in Torch involved cloning the parameters of a layer over several timesteps. The layers held hidden state and gradients which are now entirely handled by the graph itself. This means you can implement a RNN in a very “pure” way, as regular feed-forward layers.

This RNN module (mostly copied from the PyTorch for Torch users tutorial) is just 2 linear layers which operate on an input and hidden state, with a LogSoftmax layer after the output.

import torch.nn as nn

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(RNN, self).__init__()

        self.hidden_size = hidden_size

        self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
        self.i2o = nn.Linear(input_size + hidden_size, output_size)
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, input, hidden):
        combined = torch.cat((input, hidden), 1)
        hidden = self.i2h(combined)
        output = self.i2o(combined)
        output = self.softmax(output)
        return output, hidden

    def initHidden(self):
        return torch.zeros(1, self.hidden_size)

n_hidden = 128
rnn = RNN(n_letters, n_hidden, n_categories)

To run a step of this network we need to pass an input (in our case, the Tensor for the current letter) and a previous hidden state (which we initialize as zeros at first). We’ll get back the output (probability of each language) and a next hidden state (which we keep for the next step).

input = letterToTensor('A')
hidden = torch.zeros(1, n_hidden)

output, next_hidden = rnn(input, hidden)

For the sake of efficiency we don’t want to be creating a new Tensor for every step, so we will use lineToTensor instead of letterToTensor and use slices. This could be further optimized by pre-computing batches of Tensors.

input = lineToTensor('Albert')
hidden = torch.zeros(1, n_hidden)

output, next_hidden = rnn(input[0], hidden)
print(output)

Out:

tensor([[-2.9117, -3.0073, -2.9386, -2.8325, -2.9104, -2.9531, -2.8487, -2.8771,
         -2.8250, -2.9361, -2.8808, -2.9305, -2.7926, -2.8563, -2.9394, -2.9269,
         -2.8840, -2.8038]], grad_fn=<LogSoftmaxBackward>)

As you can see the output is a <1 x n_categories> Tensor, where every item is the likelihood of that category (higher is more likely).

Training

Preparing for Training

Before going into training we should make a few helper functions. The first is to interpret the output of the network, which we know to be a likelihood of each category. We can use Tensor.topk to get the index of the greatest value:

def categoryFromOutput(output):
    top_n, top_i = output.topk(1)
    category_i = top_i[0].item()
    return all_categories[category_i], category_i

print(categoryFromOutput(output))

Out:

('Polish', 12)

We will also want a quick way to get a training example (a name and its language):

import random

def randomChoice(l):
    return l[random.randint(0, len(l) - 1)]

def randomTrainingExample():
    category = randomChoice(all_categories)
    line = randomChoice(category_lines[category])
    category_tensor = torch.tensor([all_categories.index(category)], dtype=torch.long)
    line_tensor = lineToTensor(line)
    return category, line, category_tensor, line_tensor

for i in range(10):
    category, line, category_tensor, line_tensor = randomTrainingExample()
    print('category =', category, '/ line =', line)

Out:

category = Dutch / line = Ramaker
category = Dutch / line = Can
category = French / line = Beringer
category = Scottish / line = Henderson
category = Polish / line = Szwedko
category = Korean / line = Tsai
category = English / line = Blythe
category = Greek / line = Pantelakos
category = Polish / line = Kozlow
category = Dutch / line = Ogtrop

Training the Network

Now all it takes to train this network is show it a bunch of examples, have it make guesses, and tell it if it’s wrong.

For the loss function nn.NLLLoss is appropriate, since the last layer of the RNN is nn.LogSoftmax.

criterion = nn.NLLLoss()

Each loop of training will:

• Create input and target tensors
• Create a zeroed initial hidden state
• Read each letter in and
  • Keep hidden state for next letter
• Compare final output to target
• Back-propagate
• Return the output and loss

learning_rate = 0.005 # If you set this too high, it might explode. If too low, it might not learn

def train(category_tensor, line_tensor):
    hidden = rnn.initHidden()

    rnn.zero_grad()

    for i in range(line_tensor.size()[0]):
        output, hidden = rnn(line_tensor[i], hidden)

    loss = criterion(output, category_tensor)
    loss.backward()

    # Add parameters' gradients to their values, multiplied by learning rate
    for p in rnn.parameters():
        p.data.add_(p.grad.data, alpha=-learning_rate)

    return output, loss.item()

Now we just have to run that with a bunch of examples. Since the train function returns both the output and loss we can print its guesses and also keep track of loss for plotting. Since there are 1000s of examples we print only every print_every examples, and take an average of the loss.

import time
import math

n_iters = 100000
print_every = 5000
plot_every = 1000



# Keep track of losses for plotting
current_loss = 0
all_losses = []

def timeSince(since):
    now = time.time()
    s = now - since
    m = math.floor(s / 60)
    s -= m * 60
    return '%dm %ds' % (m, s)

start = time.time()

for iter in range(1, n_iters + 1):
    category, line, category_tensor, line_tensor = randomTrainingExample()
    output, loss = train(category_tensor, line_tensor)
    current_loss += loss

    # Print iter number, loss, name and guess
    if iter % print_every == 0:
        guess, guess_i = categoryFromOutput(output)
        correct = '✓' if guess == category else '✗ (%s)' % category
        print('%d %d%% (%s) %.4f %s / %s %s' % (iter, iter / n_iters * 100, timeSince(start), loss, line, guess, correct))

    # Add current loss avg to list of losses
    if iter % plot_every == 0:
        all_losses.append(current_loss / plot_every)
        current_loss = 0

Out:

5000 5% (0m 17s) 2.6763 Ybarra / Portuguese ✗ (Spanish)
10000 10% (0m 34s) 1.8967 Ceallachan / Irish ✓
15000 15% (0m 52s) 0.9030 Tang / Chinese ✓
20000 20% (1m 9s) 3.0015 Mata / Japanese ✗ (Portuguese)
25000 25% (1m 26s) 1.7356 Thien / Vietnamese ✗ (Chinese)
30000 30% (1m 44s) 3.4602 Jarzembowski / Polish ✗ (Czech)
35000 35% (2m 2s) 0.3058 Ezakiya / Japanese ✓
40000 40% (2m 18s) 0.3398 Kagawa / Japanese ✓
45000 45% (2m 35s) 1.7990 Clark / Scottish ✓
50000 50% (2m 53s) 1.8437 Melo / Spanish ✗ (Portuguese)
55000 55% (3m 11s) 0.3837 Anselmi / Italian ✓
60000 60% (3m 29s) 2.0059 Smith / German ✗ (Scottish)
65000 65% (3m 47s) 2.5846 Voigts / Greek ✗ (German)
70000 70% (4m 4s) 0.6301 Cho / Korean ✓
75000 75% (4m 21s) 0.7336 Cho / Korean ✓
80000 80% (4m 39s) 0.3585 Stevenson / Scottish ✓
85000 85% (4m 57s) 1.0549 Backer / German ✓
90000 90% (5m 15s) 0.0419 Crocetti / Italian ✓
95000 95% (5m 32s) 0.8276 Medeiros / Portuguese ✓
100000 100% (5m 50s) 1.9742 Ashbridge / Scottish ✗ (English)

Plotting the Results

Plotting the historical loss from all_losses shows the network learning:

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

plt.figure()
plt.plot(all_losses)

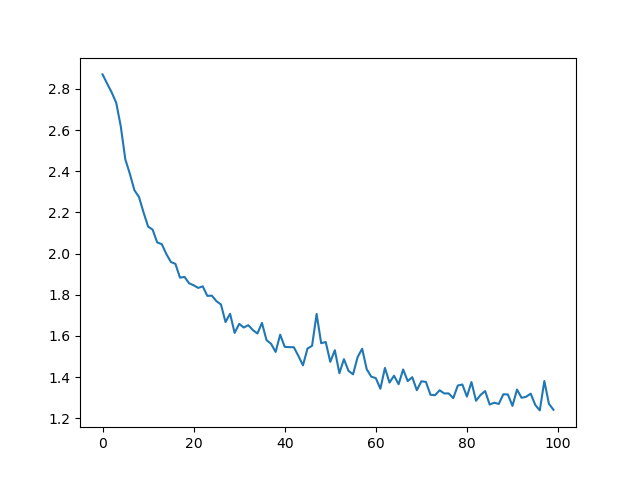
Evaluating the Results

To see how well the network performs on different categories, we will create a confusion matrix, indicating for every actual language (rows) which language the network guesses (columns). To calculate the confusion matrix a bunch of samples are run through the network with evaluate(), which is the same as train() minus the backprop.

# Keep track of correct guesses in a confusion matrix
confusion = torch.zeros(n_categories, n_categories)
n_confusion = 10000

# Just return an output given a line
def evaluate(line_tensor):
    hidden = rnn.initHidden()

    for i in range(line_tensor.size()[0]):
        output, hidden = rnn(line_tensor[i], hidden)

    return output

# Go through a bunch of examples and record which are correctly guessed
for i in range(n_confusion):
    category, line, category_tensor, line_tensor = randomTrainingExample()
    output = evaluate(line_tensor)
    guess, guess_i = categoryFromOutput(output)
    category_i = all_categories.index(category)
    confusion[category_i][guess_i] += 1

# Normalize by dividing every row by its sum
for i in range(n_categories):
    confusion[i] = confusion[i] / confusion[i].sum()

# Set up plot
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(confusion.numpy())
fig.colorbar(cax)

# Set up axes
ax.set_xticklabels([''] + all_categories, rotation=90)
ax.set_yticklabels([''] + all_categories)

# Force label at every tick
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))

# sphinx_gallery_thumbnail_number = 2
plt.show()

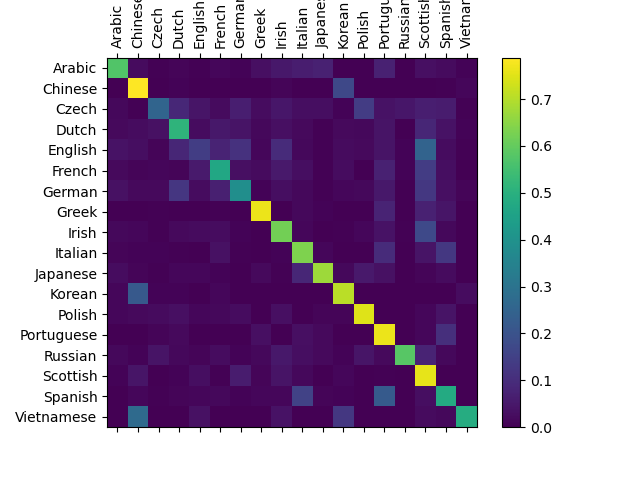
You can pick out bright spots off the main axis that show which languages it guesses incorrectly, e.g. Chinese for Korean, and Spanish for Italian. It seems to do very well with Greek, and very poorly with English (perhaps because of overlap with other languages).

Running on User Input

def predict(input_line, n_predictions=3):
    print('\n> %s' % input_line)
    with torch.no_grad():
        output = evaluate(lineToTensor(input_line))

        # Get top N categories
        topv, topi = output.topk(n_predictions, 1, True)
        predictions = []

        for i in range(n_predictions):
            value = topv[0][i].item()
            category_index = topi[0][i].item()
            print('(%.2f) %s' % (value, all_categories[category_index]))
            predictions.append([value, all_categories[category_index]])

predict('Dovesky')
predict('Jackson')
predict('Satoshi')

Out:

> Dovesky
(-0.78) Russian
(-1.34) Czech
(-1.68) Polish

> Jackson
(-0.27) Scottish
(-2.02) English
(-2.95) Russian

> Satoshi
(-1.23) Italian
(-1.35) Japanese
(-1.62) Polish

The final versions of the scripts in the Practical PyTorch repo split the above code into a few files:

• data.py (loads files)
• model.py (defines the RNN)
• train.py (runs training)
• predict.py (runs predict() with command line arguments)
• server.py (serve prediction as a JSON API with bottle.py)

Run train.py to train and save the network.

Run predict.py with a name to view predictions:

$ python predict.py Hazaki
(-0.42) Japanese
(-1.39) Polish
(-3.51) Czech

Run server.py and visit http://localhost:5533/Yourname to get JSON output of predictions.

Exercises

• Try with a different dataset of line -> category, for example:
  • Any word -> language
  • First name -> gender
  • Character name -> writer
  • Page title -> blog or subreddit
• Get better results with a bigger and/or better shaped network
  • Add more linear layers
  • Try the nn.LSTM and nn.GRU layers
  • Combine multiple of these RNNs as a higher level network